|
一、目的及重要性
系統鑑別在於獲知系統參數,進一步對系統做最佳分析與控制,因此是一項極具意義的研究課題。有鑒於許多使用上之機器是不可拆卸的,所以取得機構的參數時將會遇到困難。以下將介紹本研究室系統鑑別方法之一─基因演算法(Genetic Algorithm, GA),以供同學參考。
文中以鑑別壓電致動器作為範例,壓電材料為目前一般微動精密系統最常用的致動器,擁有耗電量少、無雜訊、體積小、反應快、發熱少、精密度佳、轉換效率高等多方面優點。但壓電元件受本身遲滯現象(Hysteresis)的影響,使驅動位移有並非完全線性的表現,因此唯有了解其特性,並獲得數學模型之參數,才能對精密系統控制做進一步的研究。
二、原理及說明
1.基因演算法的歷史
基因演算法是一種搜尋的方法,它是仿造自然界中的“物競天擇,適者生存,而弱者就會被自然淘汰”的生存競爭原則,並結合電腦科技所衍生出來的。此方法於1962年由John Holland所提出,並於1968年推出Schema定理奠定了其數學基礎。這亦使得基因演算法再1970年後被廣泛的應用在各領域中。物理方面如VLSI佈局、液晶、雷射技術等,工程方面如控制、類神經網路、模糊理論、航空、太空軌道等,其他有影像處理、蛋白質結構分析、醫學、機器人學、建築等領域之應用。基因演算法如今是進化計算發法中的一員大將,而進化計算仍在默默的發展中。
2.基因演算法的流程
基因演算法之操作過程如圖1所示。執行演算法前,先設定好各項操作參數,如:交配率(Crossover rate)、母體大小(population size)等;然後隨機產生初始染色體;之後計算各染色體的適應值(fitness function);然後依染色體適應值的大小進行複製操作,適應值較高的染色體有較大的機率被複製;當複製結束後,存活下來的染色體再進行交配及突變(mutation),以產生出下一代的染色體;如此反覆進行,直到演化結束。
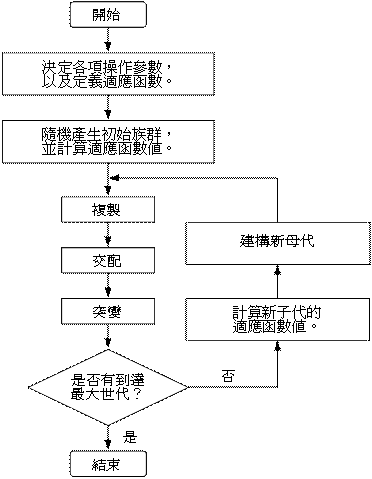
圖1•基因演算法的流程圖
|
以下對各操作做簡單的敘述:
(a) 母體大小
(b) 適應函數(Fitness function)
我們必須透過適應度函數來修正,以使得基因演算法能應用在各種不同的問題上。當然,修正後的結果必須滿足「適者生存」的觀念,亦即染色體越佳,其適應值就越高,且在演化過程中就越容易存活。
(c) 選擇機制
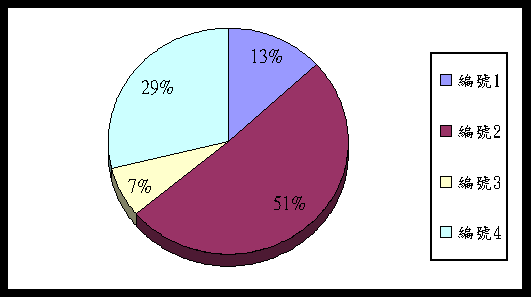
圖2•輪盤法的選擇
|
(d) 交配(Crossover)
交配操作是基因演算法重要的操作之一;它將兩個母代的部份資訊交換,而產生兩個子代;交配運算就猶如在解空間中作大幅度的跳躍搜尋。母代是否要進行交配運算取決於交配率。
(e) 突變(Mutation)
突變方式與一般演算法的鄰近區域搜尋的觀念相類似,而某染色體是否突變則取決於突變率(Mutation Rate)。在基因演算法中,藉由突變可增加母體的異樣程度,此外,突變的設定可避免落入區域解。
(f) 停止規則
為了要結束基因演算法的演化循環,我們必須預先設定停止規則,使得當遺傳演算法滿足所設定的停止規則時,則終止演化循環;常見的停止規則有以下兩種:(1)達到所設定的最大演化世代數。(2)母體內各染色體的同質性已達到預先設定的水準。所謂同質性是指非常多的染色體在相同位置上的值,完全一樣。
3. 基因演算法的優點
(a) 基因算法通常用於最佳化技術,不需太多的數學算式,由於它應用自然進 化的模式,且不需對特定系統設計發展,能處理任何種類的目標函數及任何種類拘束定義在離散、連續或混合之搜尋空間。
(b) 基因演算法是以機率的方式引導搜尋最佳解,雖然是隨機取樣,但搜尋方向必須根據適應函數隨時調整,故也非盲目搜尋。
(c) 基因演算法採平行搜尋方式,同時可以求多參數的解,較於傳統演算法更可獲得整體的最佳解,同時也避免如傳統演算法陷入區域最佳解之情形。
4. 如何將基因演算法用在系統鑑別?
首先,我們利用系統的數學模型,尋得輸入與輸出之關係,即可定義其適應函數,此適應函數為望大型態。接著,做系統鑑別時,只要取得系統輸入與輸出的資料,讓基因演算法尋求其參數,越好的參數其適應函數值會越大,這樣一代一代的衍生,我們將可取得最佳參數值,完成我們系統鑑別的工作。以下我們以鑑別含磁滯模型之壓電致動器作為例子。
典型的磁滯曲線如圖3所示。使用的磁滯模型為布斯溫模型(Bouc-Wen model),由Low和Guo於1995年簡化,如下式所示
其中V和h分別代表系統的輸入與輸出,參數 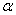 控制輸入的振幅大小,而 控制輸入的振幅大小,而 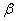 和 和 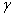 決定遲滯曲線的形狀。 決定遲滯曲線的形狀。
壓電致動器的示意圖如圖4所示,其中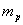 為壓電致動器等效質量, 為壓電致動器等效質量, 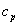 為阻尼係數, 為阻尼係數, 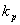 為彈簧係數以及 為彈簧係數以及 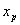 為輸出位移。其運動方程式如下 為輸出位移。其運動方程式如下
鑑別的過程如圖5所示,實際系統參數也如圖上所標示,我們可以得知輸入電壓,以及輸出位移、速度和加速度,將輸入以及輸出的資料,代入我們所定義好適應函數的基因演算法,經過60代的計算,我們可以獲得最佳參數。
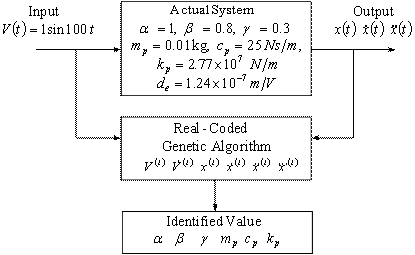
圖5•鑑別的流程示意圖
|
三、 工程應用
對於各類的機電整合系統,欲獲得其良好性能,而且具有合乎要求的穩態精度,參數的鑑別為其中之一項關鍵技術。承如第一部分所提,工業上許多機器,不論是大型操作物,或是小至微奈米級的機械元件,其大都不可拆卸,參數的取得不易。因此本研究室提供了這樣的鑑別方法,可同時鑑別各系統參數,對於工程上之應用具有貢獻。 |