|
對於工業上的應用而言，振動現象是不利的，特別是對於需要高精密度的系統。生產機器在運轉過程中所產生的振動往往會使整個機構增加疲勞破壞、噪音、降低精確度、使用壽命減少，嚴重破壞工作及環境的品質。本研究室較早期的研究重點，主要在研究各種複雜的撓性機構之暫態振動行為以及動態穩定性分析，特別是大型生產機器中的重要零組件。另外，對於移動邊界或自由邊界的問題，需要特殊的技巧及較繁複的程序來處理，問題方程式的推導及求解過程，也是研究重點之一。在分析過程中應用各種不同的分析工具如有限差分法、有限元素法以及Garlerkin方法等。曾完成分析結果的撓性機構的系統包括：高速速回機構、曲柄─滑塊機構、織帶與轉子藕合系統、電梯系統、弦線與滑塊藕合系統、黏彈性移動繩索、齒型傳送皮帶、撓性機械手臂以及磁頭與磁帶藕合系統等。
在機械振動學中，若以邊界位置、邊界之物理性質之確定與否來分類，如＜表一＞所示。一般之質量守恆系統，系統之質量固定，包含第Ⅰ、Ⅱ類。含移動邊界的機械系統，質量不守恆，系統之質量隨時間有增減，包含第Ⅲ、Ⅳ類。在＜表一＞中，
1. 第Ⅰ類中，邊界位置為固定，邊界之物理性質為已知，這一類的系統最常見，如簡支弦、樑、板等系統均是。
2. 第Ⅱ類，邊界位置為沿某曲線運動，邊界之物裡性質由幾何束縛條件可求得，如周(1992) 的滑塊曲柄機構，Beale(1988)速回機構撓性桿的運動。
3. 第Ⅲ類中，邊界位置確知，邊界之物裡性質為已知，但系統之質量隨時間有增減，如Wang 和 Wei(1987)的移動撓性機械臂的振動問題， Yuh 和Young (1991)的旋轉中的軸向移動量的動態模型。
4. 第Ⅳ類中，邊界位置為確定，邊界之物裡性質需由幾何束縛條件求得。如Fung (1993)究弦／滑塊系統，帶／輪系統，左邊界點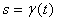 位置未確定，邊界之物裡性質由幾何束縛條件可求得，且系統之質量隨時間有增減，是屬於此類的問題。因邊界位置會移動且未確定，所引發出來的問題是，如何去推導系統之運動方程式，移動邊界位置如何去確定，又如何去求解所得的運動方程式？
|
