|
1.3 �D�u�ʼ����O�z��
1.3.1 �D�u�ʼ����O���v�T[6]
�@�@�b��K�w�챱��A�p��J�A�����O�@����]���A�ӭn�J�A�������������A���R�������欰�C�]���DzΤW�R�������欰�h�H����(dead zone)���ܡA���O�R�������欰��ڤW�O�Ѩ�عB�ʲզX�Ӧ��C�L�̤��O�O�㦳�ưʤεw�ƯS�ʪ�����ܧΡA�H�Ψ㦳�O�лP�{�H���D�u�ʼu®�ܧΡC��ʽ�i²�z�p�U�G
(1) �R�����O�O�H�ɶ��Φ�m�ܤƪ��C�o�i�H�k�]��\�h��]�A�Ҧp�ūסB�t���ܤƵ��ҷ|�y�������O���ܤơC���S�ʥ[�W���Ϫ��D�u�ʦ欰�O�ثe�b�w�챱��W�����J�A�����I�A�L�k�O�Ҩ�w�쪺���Ʋv�C
(2) ����ܧΡG���@�ܧΥD�n�㦳��j�S�ʡX�w�ƻP�ä[�ʷưʡC�o�@�{�H²�檺���N�O�ǥѷưʥͦ��F�ä[�ʪ��첾�A���o�Ǧ첾�N�|�b�I�O�����ᤴ�M�s�b�C
(3) �D�u�ʼu���ܧΡG���@�{�H�D�n�N�O���u�H�Φ��u����I���O�лP�����C�@���㪺�j��A���j��W�U�I�O�d���i�W�L��̤j�I�O�ȡC�_�h�s����ʦ첾�N�ϱo�L�k�����j���A�]����ʦ欰�P�D�u�ʼu���ܧάO��ӿW�ߪ��欰�C���첾�q�ܤp�ɡA�D�u�ʼu���ܧαN�i�����@�u�ʼu®�C���ɰt�X���ƥ����������A����t�δN�p�зǪ��G����q-�u®-�����t�ΡC
1.3.2 �����O�ҫ�������[7]
�@�@��~�ӡA�ѩ�ͤơB�b����P���q���~���i�i�A�������ת��n�D���_�a�V�W�k�ɡA�ϱo���������۷����n���u�~���C�ܩ�b�dzN��s�W�A���L��(sub-micron)�Ω`�̬��(nanotechnology)��������s�w�����G�Q�@�@�����n���dzN���СC�]���A������t�Ϊ���{�B����ת��{����s�w�����@�ӭ��n����V�C
����Ӿ���(components)��IJ�B���۹�B�ʮɡA�����O�N�|�s�b�A�p��4�ҥܡG
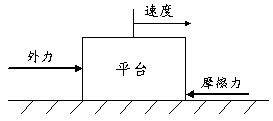
��4�E�����O�P�~�O�����Y��
|
�@�@�Y����įন���t�έ��n�����ЮɡA�����O�N�����v�T�t�κ�ת����n�]���C�W�A�����O�i�n�������R�����P�ʼ�����Ӱϰ�[8]�C����ϰ줺�����O�欰�����P�A�y�z�����O���ƾǼҫ��]�|���P�C�\�h��s���G��ܡA�����O�欰�ݩ�D�u�ʪ��ʺA�欰�F�B�]�������O�����ä��G���S�ʡA�ϱo�����O�P�ɾ֦����ܩʻP�H��m���ܪ��S��(time varying and position varying property)�y�������O�b�w�q���R�W���H�o�찪���Ʃʪ����G�C���M�w�q���R�p���A���b�w�ʤW�o�i�H�o�{�@�Ӽs�x�B�q�Ϊ��欰�ǫh�A�ӹ�5���@��`���������O�ҫ��C
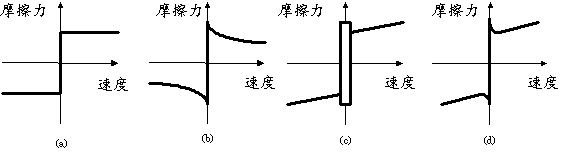
��5�E�@��`���������O�ҫ�
|
���F���i�@�B�F�Ѽ����O���ʺA�欰�A�H�U�|�T�ؼ����O�ҫ��@������s��V�G
1.3.2.1 Karnoop�����O�ҫ�[9]
�@�@
����i�u�۱�IJ���A�H������V�B�ʡA�]���b��6���A���i�P��IJ���������H��-�ưʡ]stick-slip�^�����O  �A�i�H���]��Karnopp�Ҧ�[10]�G �A�i�H���]��Karnopp�Ҧ�[10]�G
|
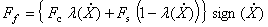
|
�]���^ |
|
�䤤 |
�@ |
|
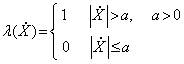
|
�]���^ |
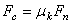 �M �M 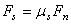 ���O���ܮw�۰ʼ����O�M�̤j�R�����O�F�� ���O���ܮw�۰ʼ����O�M�̤j�R�����O�F�� 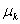 �P �P 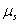 ���伯���Y�ơC�W�z���Ҧ����\�ڭ̥h�p��A�b����P�Ʀ�B�ʮɡA�Ҳ��ͪ������O�C�g���H��-�ưʼ������v���A�Ѽ� ���伯���Y�ơC�W�z���Ҧ����\�ڭ̥h�p��A�b����P�Ʀ�B�ʮɡA�Ҳ��ͪ������O�C�g���H��-�ưʼ������v���A�Ѽ� 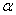 �ݧ@�O�s�F�����F�ϼƭȿn���t��k�O��í�w�A�b�ϥμƭȼ����ɡA��Ѽ�a�����O�D�s���ȡC �ݧ@�O�s�F�����F�ϼƭȿn���t��k�O��í�w�A�b�ϥμƭȼ����ɡA��Ѽ�a�����O�D�s���ȡC

��6�EKarnoop�����O�ҫ�
|
�@1.3.2.2 LuGre�����O�ҫ�[11]
�@�@LuGre�����O�ҫ��Τ@�Ӱ��Q�����A�ܼ�z�Ӵy�z�R�����O���D�u�ʦ欰�A�æb���X����ҫ��P�����O��Stribeck�����A�غc�X�@�Ө㦳����y�z���A�U�������O�欰�A��ҫ����ƾǴy�z���p�U�G
|
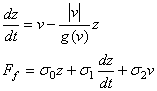
|
�]�����^ |
|
�䤤 |
�@ |
|
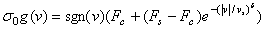
|
�]�����^ |
|
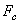 �M �M 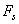 ���O���ܮw�۰ʼ����O�M�̤j�R�����O�A ���O���ܮw�۰ʼ����O�M�̤j�R�����O�A 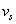 ��Stribeck�t�סA��v�����鲾�ʪ��t�סA ��Stribeck�t�סA��v�����鲾�ʪ��t�סA 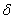 �����ƪ����N�ܼơC �����ƪ����N�ܼơC
|
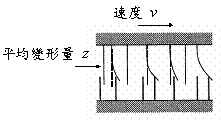
��7�E���z�פ��R�ҫ�
|
�@�@�g�ѳo�ض���ܧΪ����G�A�ӥ[�H�y�z�R�����O���ʺA�欰�A�Ӧ��ɪ����鲾�ʪ��t�״X�G�ͪ��s�A�ڭ̥i�H�Q������������]����ܧΦ��H�����A����F��̤j������ܧήɡA����~�|���Ͳ��ʳt�סA�p��8�i�������C
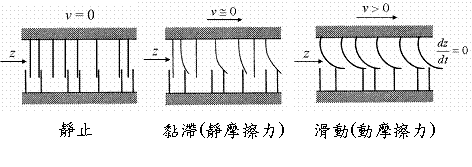
��8�E���A�ܼ�z�P�t�ת����Y��
|
�ӳ�°ʺA�U�������O�ҫ��A�i�� 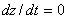 �A�ڭ̥i�H²�Ƽҫ����� �A�ڭ̥i�H²�Ƽҫ�����
|
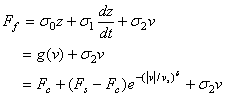
|
�]�����^ |
���ɪ������O�N�ܦ��ڭ̤@��`�����A�Ҽ{Stribeck�����Ӳ��ͫ��ƻ���H�ε��ײv�W�ɪ����u�A�p��9�ҥ�
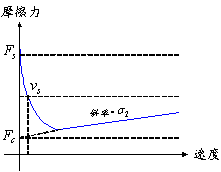
��9�E�ʺA�������O�ҫ�
|
�Y�����骺�t�� v �ͪs�ɡA�h 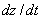 ��|���s�A���ɪ��R�A�����O�i²�Ʀ����G ��|���s�A���ɪ��R�A�����O�i²�Ʀ����G
|
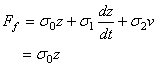
|
�]�����^ |
���ɪ����A�ܼ�z�ҳy�����R�����O�P���骺�첾�q�|���������u�A�p��10�ҥܡA�ӨëD�H�e�һ{�����P�@�ΤO���ϤO�C
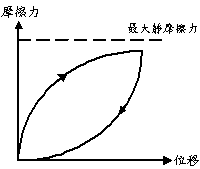
��10�E�R�A�������O�ҫ���
|
�@1.3.2.3 Leuven�����O�ҫ�[12]
�@�@Leuven�����O�ҫ��̥��O��Jan Swevers���H��2000�~�Ҵ��X���A�æb2002�@�ҫ����ץ��A��ƾǪ��y�z���PLuGre�����A���O�Ψ���p�ߪ��L����{���Һc��[13]�G
|
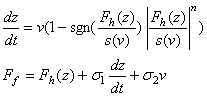
|
�]�����^ |
|
�䤤 |
�@ |
|
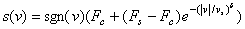
|
�]�����^ |
|
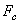 �M �M 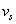 ���O���ܮw�۰ʼ����O�M�̤j�R�����O�A ���O���ܮw�۰ʼ����O�M�̤j�R�����O�A 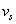 ��Stribeck�t�סA��v�����鲾�ʪ��t�סA ��Stribeck�t�סA��v�����鲾�ʪ��t�סA 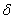 �����ƪ����N�ܼơC �����ƪ����N�ܼơC
|
�@�@Leuven�����O�ҫ��PLuGre�����O�ҫ��D�n�����P���B�A�b����R�����O���ʺA�@��s�q���ĭz�C�����N�R�����O���]�����O�A�çQ�γ����º����ҫ��Ӵy�z�����R�����O�A�p��11�ҥܡG
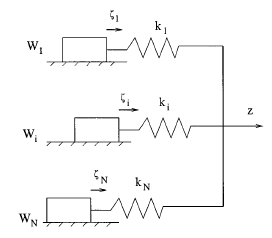
��11�E�����º��ưʼҫ�
|
�ӿ��R�����O 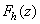 ���ƾǴy�z�����G ���ƾǴy�z�����G
|
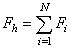
|
�]�����^ |
|
�䤤 |
�@ |
|
�@1.4 �����O�X�ʾ��c[14-17]
�@�@�����O�X�ʾ��c(Impact Drive Mechanism, IDM)�O�Q�����q���������ܧΩҲ��ͪ������ӹF��L�p�w�쪺�ت��C�����c�ȥѤ@�����q����A�@�ӥD������A�H�Τ@�ӺD����Һc���A���ݽ��������c�A�N��F��z�פW��F�쪺�L����{���L�ʯ�O�C
1.4.1 �t��
�@�@�w��Q�ν����O�@����K�w��˸m����s�A�o�i�ܤ������t�Φ��Ī̡A�����F�ʤj���T�f�б¦b1984�~�Ҵ��X���c�Q�C�̥����X����סA�O�N�q�Ͻu��(Electromagnetic Coil)�w�˦b�T�w���A�Q�ιq�e������q�Ҳ��ͪ������O�A�ΥH�X�ʪ���Ӱ���K�w��C��ӱN�q�Ͻu��w�˦b������W�A�c����ۨ��\���K�w����c�A���X�ʭ�z���Q���������q�Ͻ����O�A�P���X�ʲ�����M�κD����m���O�V�e���ʤΦV�����Y�u®�A���u®�����l���D���骺�ʯ��A�D����|�Q�u�^�æA���P������I���A�y���h�����L�ʡC���M���˸m�i��o�L�̥H�U���L�ʨB�T�A���]�u��|�o���A�H�λݤj�e�q���q�e�����D�A�]���L��Τƪ����i�C1985�~�A�n�h�������q����}�l�b�����W�c��A�H�������� �D�غc�H���q����N���q�ϤO�μu®���X�ʤ覡�C�æb1988�~�o���u�Q�����q����t�ܧΤ��W��K�w����c�v�A���X�ʤ覡�٤��������O�X�ʾ��c�A�H����S�ʥ簵��s�x�����Q�C�����O�X�ʸ˸m���L�ʨB�T�i�F�`�̯šA�w���ץi�F10�`�̡A�۸���q�ϤO���X�ʤ覡�A�ʯ�W�۷��u���A�B�L�o�������D�C
1.4.2 �X�ʭ�z
�@�@�D�������ǥѦۭ��Υ~�����O�վ���c�A�w�˦b�ưʾɤޭ��W�A�ӺD���餣�P�ɤޭ���IJ ���X�ʭ�z�A�D�Q�ι�12�ҥܤ��q���i�ΡA�����q���ͽ����O�A�óy���L�ʡC�q���i�Τ�No.1�������q�����������Ȫ��i�ΡANo.2�������q����w�C���Y�M����i�ΡANo.3�O�N�W�z��̦X�֦Ӧ����i�ΡCNo.3���i�ΩҲ��ͪ��B�T�|�j���L��̪��i�ΡC�����D������V���L�ʮɪ��L�{���� �����p�U
(1) �X�ʫe�A���q����O�b�۵M�����Y���A�C
(2) �I�����q���������ܧΪ��q���i��(�p�q���i��No.1)�Ϩ䲣�ͽ����O�A�çJ�A�@�Φb�ưʥ����W�������O�A�ϲ�����κD������O�V���ΦV�k���ʡC
(3) �H�w�C���q���i��(�p�q���i��No.2)�������q�����Y�A���ɱ���D���骺���Y�t�v���w�t�A�]�[�t���s�����ͺD�ʤO�A�ҥH�������T�w���D������i�O���b�w���ʫ᪺��m�W�C
(4) �����q�����Y�P���Ӥؤo�������A�]���ѵ��X�ʹq�������s�A�D���骺���Y�ʧ@�|��M����A���ɺD���鲣�ͤ��D�ʤO�|�A���V��������Ϩ�L�ʡC
(5) �����q���q���Y�ܭ�Ӥؤo��A�Y�����榸���X�ʰʧ@�C�t�~�A�X�ʥD������V�k�L�ʤ��X�ʹL�{�A�P�W�z��z�ۦ��A�ߦb�}�l���B�J���A���q����O�b���������A�C
��12�E�X�ʹq�����i��
|
�Q�ΤW�z���X�ʭ�z�A�D������i�F�췥����K���L�ʨB�T�C�Y�s���X�ʥD������V�����ʡA�h�u�ݭ��ƬI�[�ۦP���q���i�Φ����q����C�߽Ħۨ����c�C���X�ʮɩҲ��ͪ��첾�q�i�q�Ʃ`�̨�ƷL�̡C
1.4.3 �����O�X�ʾ��c���R�A�S�ʤΰʺA�S��
�@�@
�����礧�ت��D���T�{�ưʥ��i�̨Ϊ��w���סA�H�δ��շưʥ��i�̲ת����ijt�סC�ҿ��R�A�S�ʬ��榸�X�����q����ɪ����ʯS�ʡA�ӰʺA�S�ʬ��s���X�����q����ɪ����ʯS�ʡC
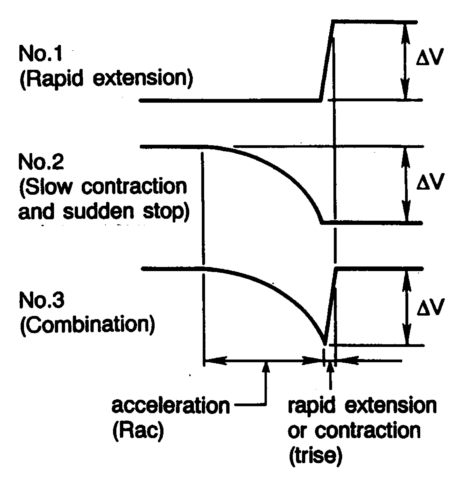
�p��13�ҥܡA�b�R����A�ɡA�����O�伵��������(�YMass����)�A�ӺD����(�YWeight����)�����۩����q���ƥt�@�ݤ���q���C���ɧY�i�N�w����c�����@�����O�X�ʾ��c�A�㥪�k�L�ʪ��\��C���X�ʭ�z�A�Ѧҹ�16���X�ʹq�����i�ΥH�ι�14���X�ʭ�z�A�y�z�p�U�G
�]a�^�X�ʫe���q����O�b���Y���۵M���A�C
�]b�^�I�����q�����������Ȫ��q���i�Ρ]�p�q���i�Ϊ�No.1�����^�Ϩ䲣�ͽ����O�A�çJ�A�@�Φb�ưʥ��i�W�������O�A�ϲ�����M�κD����m���O�V���ΦV�k���ʡC
�]c�^�H�w�C���q���i�Ρ]�p�q���i�Ϊ�No.2�����^�������q�����Y�A���ɱ���D���骺���Y�t�v���w�t�A�]�[�t���s�����ͺD�ʤO�A�ҥH�������T�w��������i�O���b�w���ʫ᪺��m�W�C
�]d�^�����q�����Y�ܨ��Ӥؤo�������A�]���ѵ��X�ʹq�������s�]�p�q���i�Ϊ�No.3�����^�A�D���骺���Y�ʧ@�|��M����A���ɺD���鲣�ͤ��D�ʤO�|�V��������Ϩ�A���L�ʡC
�]e�^�����q�����Y�ܨ��Ӥؤo��A�Y�����榸���X�ʰʧ@�C�t�~�A�X�ʷưʥ��i�V�k�L�ʤ��X�ʭ�z�A�P�W�z��z�ۦ��A�߶}�l���B�J���A���q����O�b���Ȫ����A�C
�V�����ʡ@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�V�k����
��14�E�ۨ����c(IDM)���X�ʭ�z
|
�Q�ΤW�z���X�ʭ�z�A�ưʥ��i�i�F�췥����T���L�ʨB�T�C�Y�s���X�ʷưʥ��i�V���A�h���ƬI�����q����ۦP���q���i�ΡA�i��o�}�n���ʺA���ʯS�ʡC�ھ�IDM�X�ʸ˸m�����絲�G���i�A���ѯ�i�F1�`�̡A�w���ץi�F10�`�̡C
1.4.4 XY�G�ۥѫשw��t�Ϋإ�
1.4.4.1 �w��t�ά[�c
�@�@�ѩ�{�b�����~�O�V�ӶV��p�A�]���[�u���x���\��γt�קֳt�����ɡA���XY���x�]�H���A�D�\�ണ�ɡCXY��K�w��ƥx�A�b�]�p���q���Ҽ{�~�ε��c��²��ơB�B�ʥ��骺���q�ơB�ΧC�D�ʯx�B�ƥx���骺����ʡB���T���ʡB���ܧΤp�Ϊ��ɶ��ϥιةR���S�ʡC�H���bXY���x���A�`�ϥξ�������X�ʡA�@�볣�O�α���P�����F�a�ʾ�����A�N����B�ʪ������ܬ����u�B�ʡC���O�A�H�����줧�ƥx�B�ʳt�צb�t�X���ড�P�����F��A��t�ר������̤j�~�V�O�b������쥻����Ө����̤j�t�[�סC�H�ۺu�]��������t�������A�N�v���������쪺�۵M�W�v�A���Y�ް_�@���{���A�Ӥ����~����ʡC�ҥH�ϥξ����쪺��t�A���������b�@�����{����t�H�U�C�ӥB������b�M�����Ψ�L�s��t�X����ɡA��������I�ؤξ�����u���ܧΩҲ��ͪ��~�t�C�]���A���ت��X�ʤ覡��{�b�A�D��������H�F��C
�@�@�H�ثe�f�t�u�ʷƭy��XY�ƥx�A���Q�κu�ʶb�Ӥή����b�Ө�ءA�]�p�ɥ����Ҽ{���]���������B���ƫO�i�ɮġB���t�B��ɺ�O���B�@�����S�ʡB�Ů�����í�w�M��������C�t�~�Ҽ{�ƥx���c�b�Ұʩΰ���ɤ����[��t�B�ʩΰ��t�B��ɡA�Ҳ��ͤ��C�W�@���{���A�ѩ{�����y���ƥx�w���ת��}���A�ҥH�]�p���q�i�Q���W�v�T���k�q�����C�W�@���I�A�b�]�p����ɥi�ѰѦҡC
�b���@�ۥѫפU�������O�X�ʸ˸m�@��Өt�γ̨ΤƳ]�p��A�ڭ̦b�إߥXXY�G�ۥѫשw�쥭�x���[�c�A�öi��[�u�P���U�Ӫ���s���ءC���w��t�Υثe�N��B�]�p����ս����O�X�ʸ˸m���X�Ӧ��A�C�@���X�ʸ˸m�x����@�ۥѫת��w��A��өw��t�ά[�c�p��15�ҥܡG
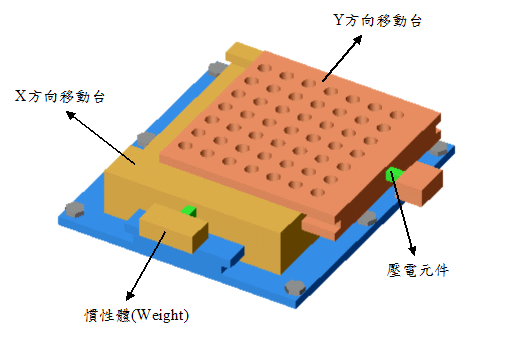
��15�E�G�ۥѫשw�쥭�x�[�c��
|
�@1.4.4.2 ����˸m�إ�
�@�@���G�ۥѫ���˸m�����n���D�O�A�p��H���g�٤��]�Ʀ����A�c�v�̨Ϊ�����Ҧ��A�F�쨳�t�w�줧�ت��A�H���Ѳ��~������ΡC�w�w������ؼЬ��A�b10�����F��10 nm���w���סC�b�����q�ҳ]�p����`�̯Ū��w��t�ΡA�����W�G�ۥѫײ��ʪ��������Y�A�]���C�@�b�]�ҦpX�b�^����¹B�ʡA���i��|�y���t�@�b���z�A�B�ʡC�Y�Ҽ{�z�A�B�ʮɪ�����Ҧ����������A�]���A�����q�D�n���Q�����D�A�O�p��H�̦��g�٤γ̦��IJv������覡�A�F�찪��פΰ��w��t�v���n�D�C�����q�D�W��PC-Based������t�ΡA�Q�ΦU�ؤ��P��������A�����b�۰ʩw��ʯ�W���u�H�C�t�~�A�������i���X�ʭ�z�A�D�O�Q�����q���������ܧΩҲ��ͪ������O�C�����[�c�Ϧp��16�ҥܡG
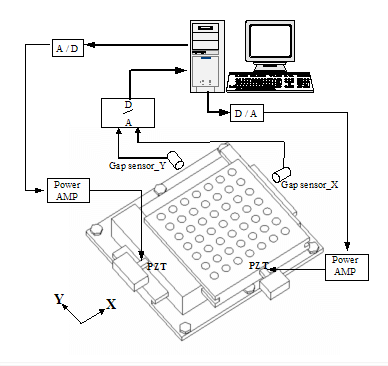
��16�E�w��t���[�c��
|
�@
�T�B �u�{����
�@�@����s���嫬�u���q��X�v�����D�A��Y�]�t���]�p�B�s�y�A���q���ഫ�����R�����ΡA�P�����P����t�Ϊ���X�A�q�������]�p�A�H�δ��z������t�Τ��ɤJ����X�N�����ΡC�]���A���ѻP���u�@�H���A��b���q��X���W�o�짹�㪺�V�m�A�ï�Ϩ���{��K�q���P����b��a��o�i�W�����n�ʡC�ר�A����s���λ��ȡA�Ұ��i���N�A�൲�X�ǬɻP���~�ɦ@�P�i�����ά�s�A�ô��Ѷ}�ҹ�`�̥@�ɧǹ�����¦�N�A����ʧڰꥼ�Ӻ�K�u�~���o�i�A���ɰ���v���O�����^�m�C
�@
�ѦҤ��m
[1] ���a�ץD�s�A2002�A�`�L�̤u�{-��K�s�{�P�q���N�A�ɮ��ѧ��C
[2] �����s�B���a�ץD�s�A2002�A�`�̤u�{�N�A�ɮ��ѧ��C
[3] ���a�סB�����K�D�s�A2003�A�`�̤u�{���סA���خѧ��C
[4] ���Ǥ��A2003�A�u��D��٩ʺϺ��t�α���Ψ�����q�X�ʥ��x�w�챱����Ρv�A��ߦ��\�j�ǡA��ŤӪŤu�{�t�A�Ӥh�פ�A�����O�б«��ɡC
[5] Low, T. S., and Guo, W., 1995, ��Modeling of three-layer piezoelectric bimorph beam with hysteresis��, IEEE Journal of Microelectromechanical Systems, 4, (4), pp. 230-237.
[6] ���a�סB�������B�����I�A2003�A���Ϻ��P�����O�Ҽ{���`�̩w�졨�A���z����Z�G�Q����T���C
[7] Fung, R. F. and Han, C. F., 2003, ��Effects of Frictional Models on the Dynamic Responses of an Impact Drive Mechanism��, Proceedings of the 27th Conference on Theoretical and Applied Mechanics, 1, pp. 1-8.
[8] Armstrong-Helouvry, B., Dupont, P., and Canudas de Wit, C., 1994, ��A survey of models, analysis tools and compensation methods for the control of machines with friction��, Automatica, 30, (7), pp. 1083-1138.
[9] Karnopp, D., 1985, ��Computer simulation of stick-slip in mechanical dynamic system��, ASME Journal of Dynamic Systems, Measurement, and Control, 107, pp. 100-103.
[10] Cao, L., and Schwartz, H. M., 2000, ��Stick-slip friction compensation for PID positioncontrol��, Proceeding of the American Control Conference, pp. 1078-1082.
[11] Canudas de Wit, C., Olsson, H., , K., and Lishinsky, P., 1995, ��A new model forcontrol of systems with friction��, IEEE Transactions on Automatic Control, 40, pp. 419-425.
[12] Swevers, J., Al-Bender, F., Ganseman, G., and Prajogo, T., 2000, ��An integrated friction model structure with improved presliding behavior for accurate friction compensation��, IEEE Transactions on Automatic Control, 45, pp. 675-686.
[13] Lampaert, V., Swevers, J., and Al-Bender, F., 2002, ��Modification of the Leuven integrated friction model structure��, IEEE Transactions on Automatic Control, 47, (4), pp. 683-687
[14] Higuchi, T., Furutani, K., Yamagata, Y., Kudoh, K., and Ogawa, M., 1993, ��Improvement of velocity of impact drive mechanism by controlling friction,�� Journal of Advanced Automation Technology, 5, (2), pp. 71-76.
[15] Liu, Y. T., Higuchi, T., and Fung, R. F., 2003, ��A novel precision positioning table utilizing impact force of spring-mounted piezoelectric actuator �V part I: experimental design and results,�� Precision Engineering, 27, pp. 14-21.
[16] Liu, Y. T., Higuchi, T., and Fung, R. F., 2003, ��A novel precision positioning table utilizing impact force of spring-mounted piezoelectric actuator �V part II: theoretical analysis,�� Precision Engineering, 27, pp. 22-31.
[17] Fung, R. F., Liu, Y. T., and Huang, T. K., 2003, ��Dynamic responses of a self-moving precision positioning stage impacted by a spring-mounted piezoelectric actuator,�� ASME Journal of Dynamic Systems, Measurement, and Control, 125, pp.658-661.
|